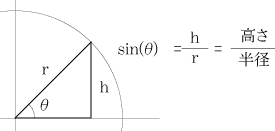たわごと

数学とパズル

最近(というわけでもないが)、数学の本を買ってしまいました。次の図はご存知、三角関数。今の仕事でもかなり使ってます。知らないうちにCAD等でもフル活用していると思われる。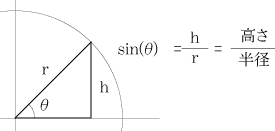
今頃間違いに気が付きました。高さh÷半径r、ですね。

どうやって直径を測るのさ

次の図のような物体があります。中心を通る対角線上に直径円に接する部分があればノギスなどで寸法を測ることができるのですが、対角線上にない場合、どうやって直径を測ったらよいでしょうか。フランジと穴があり、直径円に接する部分は3ヶ所とは限りません(1ヶ所だけの場合もあります)。この物体は奇数の歯数を持つ歯車やカムのようなものだと考えてよいでしょう。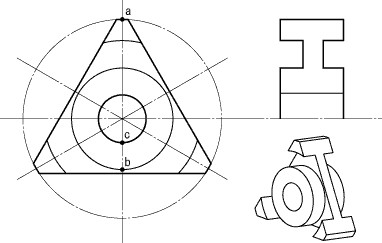

数学的にはどうかわかりませんが(ちゅんさんゴメン)、どうにかして直径が測れればいいのでパズル的に簡単に考えてみます。フランジbの真円度が期待できる場合に限りますが、頂点aとフランジbの対角線の寸法=α,フランジbの直径=βをそれぞれノギスで測ります。そしてα×2-βが頂点aを通る外径円の直径寸法になるはずです。フランジbの代わりに穴にシャンクcを通した場合にも同様に求められます。似たような方法で頂点aとフランジbの差の寸法=γがわかった場合はγ×2+βになります。

どうやって円の中心を求めるのさ

次の円の円周上に3つの点があります。その3つの点A，B，Cの座標を (x_A,y_A) (x_B,y_B) (x_C,y_C) とすると、円の中心Oの座標 (x_O,y_O) はどうやって求めたらいいのでしょうか。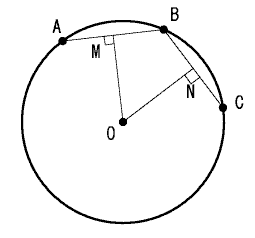

まず線分ABの中点Mを通り線分ABに垂直な線は円の中心Oを通過する。点A点Bの座標を平均して線分ABの中点M、線ABの定義式より線ABの傾きが求まる。これらより線OMの定義式が求まる。同様に線分ONの定義式も求まる。線OMと線ONの定義式を連立方程式として式をx,yについて展開していくと、線OMと線ONの交点すなわち円の中心Oの座標 (x_O,y_O) が求められる。――他にも方法はあると思いますが(円の定義式3つの連立方程式かなぁ?)、これはこれで解きやすいような気がします。求めた式は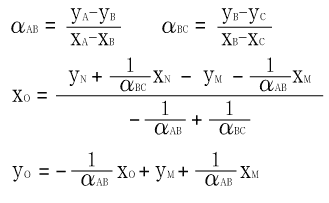

・・・から・・・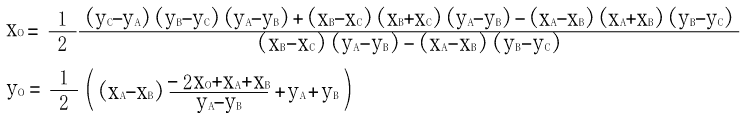

・・・たぶん。

xo = ((yc-ya)*(yb-yc)*(ya-yb)+(xb-xc)*(xb+xc)*(ya-yb)-(xa-xb)*(xa+xb)*(yb-yc)) / ((xb-xc)*(ya-yb)-(xa-xb)*(yb-yc)) / 2.;
yo = ( (xa-xb)*(-2.*xo+xa+xb)/(ya-yb)+ya+yb ) / 2.;

イメージマップ 〜 ある点が三角形の中にあるか 〜

イメージマップ、よく使われています。画像の中のどこかをクリックすると他のページへジャンプしたりします。あれってクリックした点が、ページ作成者の指定するどの図形の中に入っているかでジャンプ先を振り分けています。で・・・「図形の中に点が入っているか」ということなのですが、

• 円は円の定義式の応用x²+y² < r²でわかる
• 四角形は座標の大小関係だけでわかる
• じゃあ多角形は・・・？

多角形は三角形の集まったもの、と考えることが出来ます。ではある点Pが三角形ABCの中にあるかどうか判断する方法はどうしたらよいでしょうか？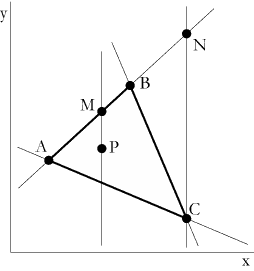

まず線ABと点Pの関係に着目します。点Pが三角形ABCの中にありそうな条件は、線ABを境界線として点Pが点Cと同じ側にあるということです。これを判断するには線ABの定義式より関数y=ƒ_AB(x)を用意しておき、y_Pに対するƒ_AB(x_P)すなわちy_Mと、y_Cに対するƒ_AB(x_C)すなわちy_Nの大小関係が同じになればよいということです。これを他の2つの線分に対しても同様に行い、総てクリアすれば点Pが三角形ABCの中にあるということです。もちろん線の定義式がy=定数､x=定数の場合は座標から大小関係を判断しないと電子計算機ではエラーになるので注意。

トップページへ